こんな問題はどうでしょう??(中学生:塾だより1-2月号)
見た目はシンプル・・・
こんな問題はどうでしょう??
※クリックすると拡大されます。
(多田先生)
解答
数学の勉強で「解く」問題には二種類あると思うのです。ひとつはすぐ解答・解説を見たり先生に聞いたりして速攻で解決すべき問題。もうひとつは何日も何週間も何か月もかけていいから自力で解くべき問題。特に基礎を身につける段階ではすぐ解答・解説を見ることが大切ですね。証明とか採点していると、言いたいことはわかるけど表現が「なんじゃこれ!?」というものが時々あります。いろいろな習い事と同じように基礎、模範となるものをしっかり「真似する」練習をしていないからだと思います。
一方、数学の世界では何十年、何百年もかけてようやく解けるような問題があります。「フェルマーの最終定理」「ポアンカレ予想」「abc予想」などネットで検索すると面白い話がぞくぞく出てきます。さらに人類が未だに解決できない問題も無数にこの世には存在してます。(なんて壮大な話だと思いませんか?)
自分で問題を解こうとするとき、あらゆる道具(今まで習った知識)を駆使して攻略しようとします。ゲームと同じですね。
そのとき脳内では知識の検索と整理、総復習、定着がフルパワーで行われているわけです。だからもし解けなくても学力は飛躍的に向上し、解けたときには達成感・自信感は半端ないですね。だからボクは解きたい(知りたい)問題のテーマをいつも持っています。その中に「ガロアの理論」「バナッハ・タルスキーの定理」などあります(恥ずかしながら未だに完璧に理解していないので)。
難しい言葉をいろいろ並べてしまいすみません。けれど高校・大学などへ進学したらぜひ一度は目に触れてほしい言葉です。その背後にある人間の歴史もまたドラマチックですから。
勉強方法については「これが絶対」というものはないんじゃないかなぁと思っていて、十人十色、人それぞれに最適な方法があるのではないかと。だからここに書いた数学の勉強方法も「そういう手もあるか」程度でいいので参考にして試してみてくれると嬉しいなと思います。
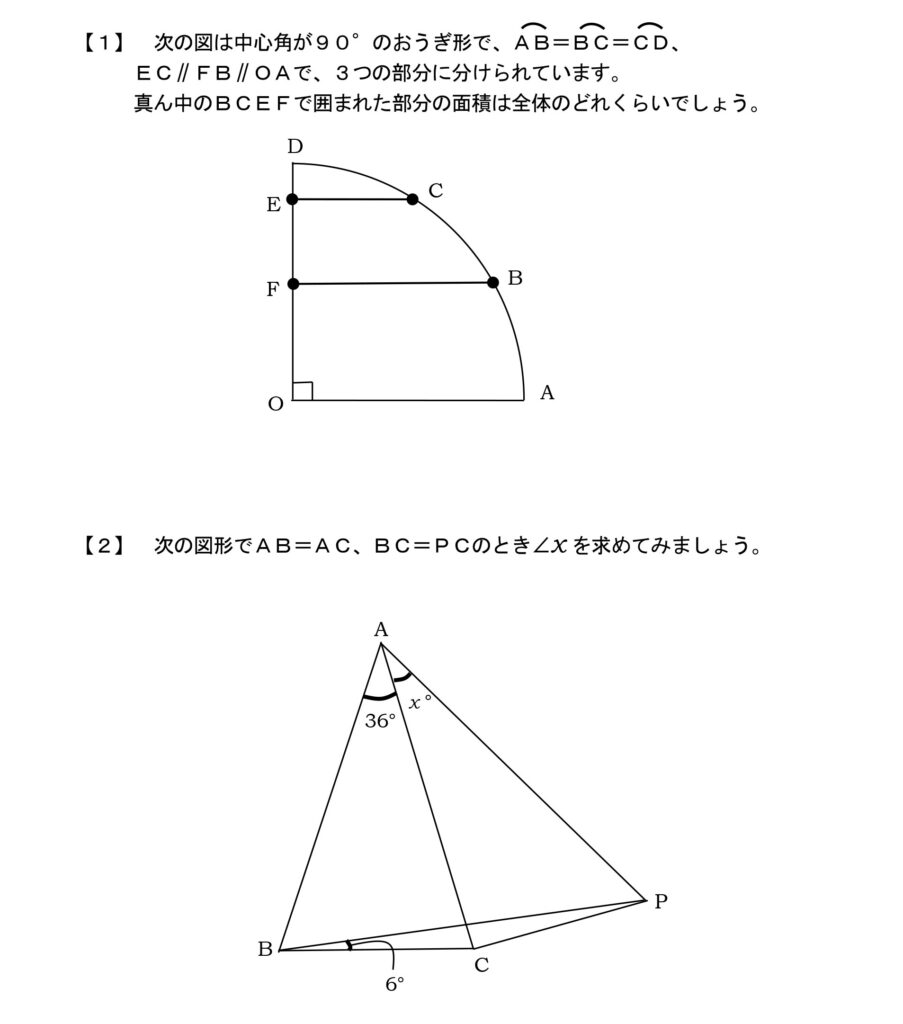
【1】
二分の一は1/2 三分の一は1/3
などと表記することにします
CからOAに引いた垂線と
FBとの交点をGとする
△COG=△CFG=1/2 EFGC
△COG=△BOG
おうぎ形OBCと等しくなるので1/3
【2】
すぐに分かる角度や等しい線分
は略します。
CB=CQ、∠BCQ=108°
となる点Aに近いほうの
点をQとする
ACとBQの交点をRとする
∠CBQ=∠CQB=36°
△BRC≡△ARQ
(二辺とその間の角)
∠CAQ=36°、∠QCP=60°
AQ=CQ=CB=CP=PQ
∠AQP=168°、∠PAQ=6°
∠x =30°
中3生は円周角を用いると
もっとすっきりできます。
- カテゴリー
- 塾だより